CD's blog
CD
2021-08-21
目录

每日一题

# 丑数系列

什么是丑数？

丑数就是只包含质因数 2, 3, 5 的正整数。0 和负整数一定不是丑数。 输入：不会超过 32 位有符号整数的范围: [−2^31, 2^31 − 1]。 对于任意一个丑数 x，其与任意的质因数（2、3、5）相乘，结果（2x、3x、5x）仍为丑数

# 263. 丑数(简单)

给你一个整数 n ，请你判断 n 是否为 丑数 。如果是，返回 true ；否则，返回 false 。

丑数 就是只包含质因数  2、3 和/或  5  的正整数。

示例 1：

输入：n = 6 输出：true 解释：6 = 2 × 3 示例 2：

输入：n = 8 输出：true 解释：8 = 2 × 2 × 2 示例 3：

输入：n = 14 输出：false 解释：14 不是丑数，因为它包含了另外一个质因数  7 。 示例 4：

输入：n = 1 输出：true 解释：1 通常被视为丑数。

思路： 为判断 nn 是否满足上述形式，可以对 nn 反复除以 2,3,5，直到 n 不再包含质因数 2,3,5。若剩下的数等于 1，则说明 n 不包含其他质因数，是丑数；否则，说明 n 包含其他质因数（除了自身和 1 不能被其他数整除的数），不是丑数。

/**
 * @param {number} n
 * @return {boolean}
 */
var isUgly = function(n) {
  if (n <= 0) return false;
  [2, 3, 5].map(i=>
    while(n % i === 0) {
      n = n / i
    }
  );
  return n === 1
};
1
2
3
4
5
6
7
8
9
10
11
12
13

# 264. 丑数 II(中等)

给你一个整数 n ，请你找出并返回第 n 个 丑数 。

丑数 就是只包含质因数  2、3 和/或  5  的正整数。

示例 1：

输入：n = 10 输出：12 解释：[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。 示例 2：

输入：n = 1 输出：1 解释：1 通常被视为丑数。

提示：

1 <= n <= 1690

思路：

  1. 优先序列(小根堆)
  • 起始先将最小丑数 1 放入队列
  • 每次从队列取出最小值 x，然后将 x 所对应的丑数 2x、3x 和 5x 进行入队。
  • 对步骤 2 循环多次，第 n 次出队的值即是答案。
  1. 多路归并（多指针）解法 我们「往后产生的丑数」都是基于「已有丑数」而来（使用「已有丑数」乘上「质因数」2、3、5）。 因此我们可以使用三个指针来指向目标序列 arr 的某个下标（下标 0 作为哨兵不使用，起始都为 1），使用 arr[下标] * 质因数 arr[下标]∗ 质因数 代表当前使用到三个有序序列中的哪一位，同时使用 idx 表示当前生成到 arr 哪一位丑数。
/**
 * @param {number} n
 * @return {number}
 */

// 优先序列
var nthUglyNumber = function (n) {
  const ints = [2, 3, 5];
  const sets = new Set();
  const arrs = [];
  sets.add(1);
  arrs.push(1);
  for (let i = 1; i <= n; i++) {
    const res = arrs.shift();
    if (i === n) return res;
    for (let j of ints) {
      const t = j * res;
      if (!sets.has(t)) {
        sets.add(t);
        arrs.push(t);
        arrs.sort((a, b) => {
          return a - b;
        });
      }
    }
  }
  return -1;
};

// 多路归并（多指针）解法
var nthUglyNumber = function (n) {
  const arr = new Array(n + 1);
  arr[1] = 1;
  const xx = [2, 3, 5];
  for (let i1 = 1, i2 = 1, i3 = 1, idx = 2; idx <= n; idx++) {
    const id1 = arr[i1] * 2;
    const id2 = arr[i2] * 3;
    const id3 = arr[i3] * 5;
    const minValue = Math.min(id1, id2, id3);
    id1 === minValue && i1++;
    id2 === minValue && i2++;
    id3 === minValue && i3++;
    arr[idx] = minValue;
  }
  return arr[arr.length - 1];
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# 313. 超级丑数 (opens new window)

超级丑数 是一个正整数，并满足其所有质因数都出现在质数数组 primes 中。

给你一个整数 n 和一个整数数组 primes ，返回第 n 个 超级丑数 。

题目数据保证第 n 个 超级丑数 在 32-bit 带符号整数范围内。

示例 1：

输入：n = 12, primes = [2,7,13,19] 输出：32 解释：给定长度为 4 的质数数组 primes = [2,7,13,19]，前 12 个超级丑数序列为：[1,2,4,7,8,13,14,16,19,26,28,32] 。 示例 2：

输入：n = 1, primes = [2,3,5] 输出：1 解释：1 不含质因数，因此它的所有质因数都在质数数组 primes = [2,3,5] 中。

提示：

1 <= n <= 106 1 <= primes.length <= 100 2 <= primes[i] <= 1000 题目数据 保证 primes[i] 是一个质数 primes 中的所有值都 互不相同 ，且按 递增顺序 排列

// 动态规划
var nthSuperUglyNumber = function (n, primes) {
  const dp = new Array(n + 1).fill(0);
  dp[1] = 1;
  const m = primes.length;
  const pointers = new Array(m).fill(1);
  for (let i = 2; i <= n; i++) {
    const nums = new Array(m).fill(m);
    let minNum = Number.MAX_SAFE_INTEGER;
    for (let j = 0; j < m; j++) {
      nums[j] = dp[pointers[j]] * primes[j];
      minNum = Math.min(minNum, nums[j]);
    }
    dp[i] = minNum;
    for (let j = 0; j < m; j++) {
      if (minNum == nums[j]) {
        pointers[j]++;
      }
    }
  }
  return dp[n];
};
// 最小堆
var nthSuperUglyNumber = function (n, primes) {
  const sets = new Set();
  const arrs = [];
  arrs.push(1);
  sets.add(1);
  for (let i = 1; i <= n; i++) {
    const item = arrs.shift();
    if (i === n) return item;
    for (let j of primes) {
      if (!sets.has(j * item)) {
        sets.add(j * item);
        arrs.push(j * item);
        arrs.sort((a, b) => a - b);
      }
    }
  }
  return -1;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

# 等差数列划分

如果一个数列 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该数列为等差数列。

例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 nums ，返回数组 nums 中所有为等差数组的 子数组 个数。

子数组 是数组中的一个连续序列。

示例 1：

输入：nums = [1,2,3,4] 输出：3 解释：nums 中有三个子等差数组：[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。 示例 2：

输入：nums = [1] 输出：0

提示：

1 <= nums.length <= 5000 -1000 <= nums[i] <= 1000

思路：

  • 动态规划：动态规划方程 - 上上次的差值和上次的差值相同的时候就会是等差数列，不断累加。
// 动态规划
var numberOfArithmeticSlices = function (nums) {
  let sum = 0,
    l = 0;
  for (let i = 2; i < nums.length; i++) {
    if (nums[i - 2] - nums[i - 1] === nums[i - 1] - nums[i]) {
      l++;
    } else {
      l = 0;
    }
    sum += l;
  }
  return sum;
};

// 差值划分
var numberOfArithmeticSlices = function (nums) {
  if (nums.length <= 1) return 0;
  let ex = nums[0] - nums[1],
    t = 0,
    sum = 0;
  for (let i = 2; i < nums.length; i++) {
    if (nums[i - 1] - nums[i] === ex) {
      t++;
    } else {
      t = 0;
      ex = nums[i - 1] - nums[i];
    }
    sum += t;
  }
  return sum;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# 446. 等差数列划分 II - 子序列

给你一个整数数组 nums ，返回 nums 中所有 等差子序列 的数目。

如果一个序列中 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该序列为等差序列。

例如，[1, 3, 5, 7, 9]、[7, 7, 7, 7] 和 [3, -1, -5, -9] 都是等差序列。 再例如，[1, 1, 2, 5, 7] 不是等差序列。 数组中的子序列是从数组中删除一些元素（也可能不删除）得到的一个序列。

例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。 题目数据保证答案是一个 32-bit 整数。

示例 1：

输入：nums = [2,4,6,8,10] 输出：7 解释：所有的等差子序列为： [2,4,6][4,6,8] [6,8,10][2,4,6,8] [4,6,8,10][2,4,6,8,10] [2,6,10] 示例 2：

输入：nums = [7,7,7,7,7] 输出：16 解释：数组中的任意子序列都是等差子序列。

提示：

1  <= nums.length <= 1000 -231 <= nums[i] <= 231 - 1

由于这道题我知道要用动态规划做，但是水平有限，所以学习了 liweiwei1419 大佬的思路，容我 copy 一份做学习

以「示例 1」 为例 下面的描述重点在：「公差」相等的时候，才可以接上去，并且注意看一下是到哪个状态的哈希表里找（我加了着重号）。并且大家留意一下是如何计算结果的（和上面那张图的计算方法一模一样）。

哈希表的「键」的含义是「公差」。

输入：nums = [2, 4, 6, 8, 10]。

整个过程形成的键值对如下：

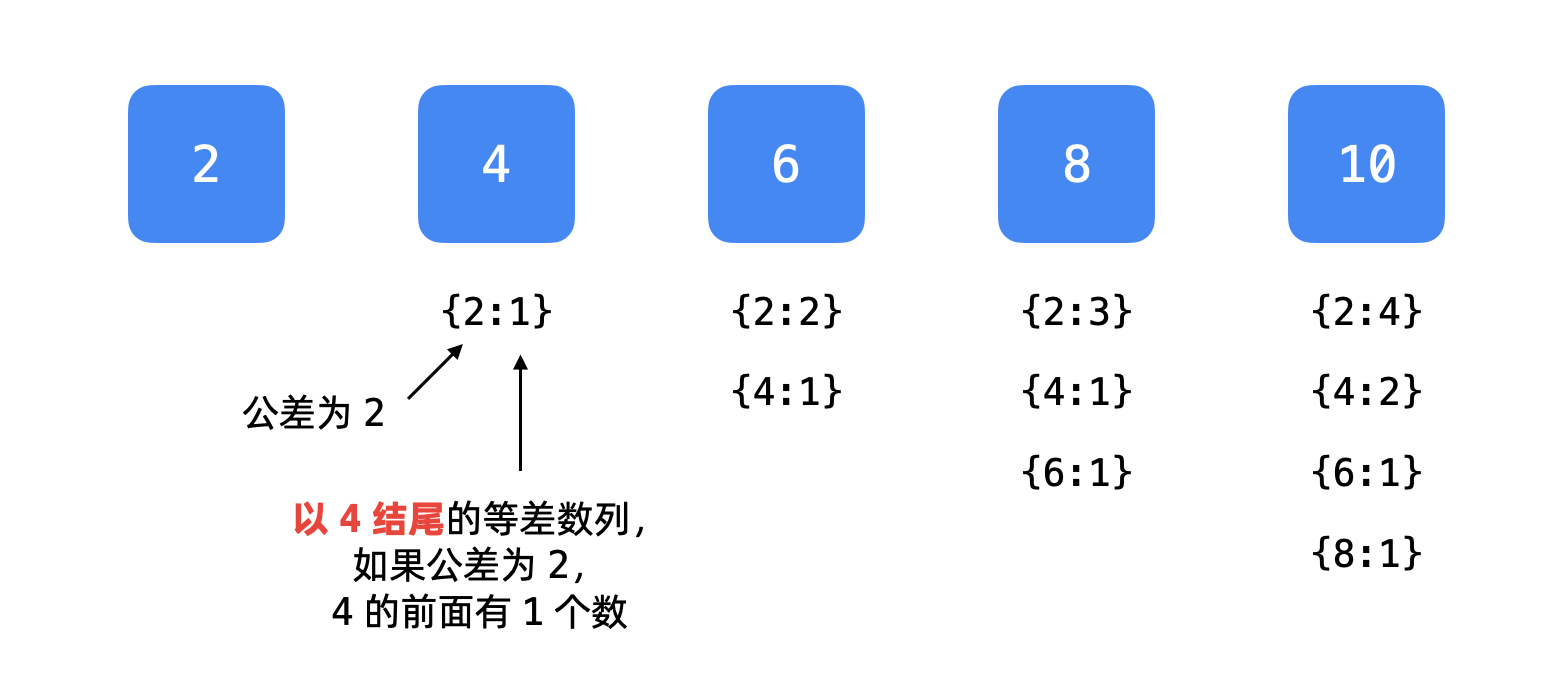pic 下面逐个解释：

  • 2 的前面没有元素，哈希表为空；

  • 4 的前面只有一个元素 2 ，此时记录键值对 {2:1}，这里 2 是「公差」，1 是 4 前面的元素的个数；

  • 6 的前面有两个元素 4 和 2：

    • 6 - 4 = 2，在 4 的键值对里看一下，有 2，说明 6 可以接在 4 的后面形成长度更长的等差数列 [2, 4, 6]，此时记录记录键值对 {2:2}，同时找到了一个长度为 33 的等差数列；
    • 6 - 2 = 4，在 2 的键值对里看一下（看第 1 条，哈希表为空），没有 4，此时记录 {4:1}；

  • 8 的前面有三个元素 6、4 和 2：

    • 8 - 6 = 2，在 6 的键值对里看一下，有 2，说明 8 可以接在 6 的后面形成长度更长的等差数列，此时记录键值对 {2:3}，同时找到了两个长度大于等于 33 的等差数列 [4, 6, 8] 和 [2, 4, 6, 8]（这里的 2 个是基于 6 的状态值 + 1 得到的，与 413. 等差数列划分 题一样，可以看上面唯一的一张图，不展开解释了）；
    • 8 - 4 = 4，在 4 的键值对里看一下，没有 4，记录 {4:1}；
    • 8 - 2 = 6，在 2 的键值对里看一下，没有 6，记录 {6:1}；

  • 10 的前面有四个元素 8、6、4 和 2：

    • 10 - 8 = 2，在 8 的键值对里看一下，有 2，说明 10 可以接在 8 的后面形成长度更长的等差数列，此时记录记录键值对 {2:4}，同时找到了两个长度大于等于 33 的等差数列 [6, 8, 10] 、 [4, 6, 8, 10] 和 [2, 4, 6, 8, 10]（这里的 3 个是基于 8 的状态值 + 1 得到的；
    • 10 - 6 = 4，在 6 的键值对里看一下，有 4，说明 10 可以接在 6 的后面形成长度更长的等差数列，此时记录记录键值对 {4:2}，同时找到了一个长度大于等于 33 的等差数列 [2, 6, 10]；
    • 10 - 4 = 6，在 4 的键值对里看一下，没有 6，记录 {6:1}；
    • 10 - 2 = 8，在 2 的键值对里看一下，没有 8，记录 {8:1}。

可得代码:

var numberOfArithmeticSlices = function (nums) {
  const n = nums.length;
  const hash = new Map();
  let sum = 0;
  for (let i = 0; i < n; ++i) {
    hash[i] = new Map();
  }
  for (let i = 1; i < nums.length; i++) {
    for (let j = 0; j < i; j++) {
      const res = nums[i] - nums[j];
      const l = hash[j].get(res) || 0;
      sum += l; // 如果res已经在之前有存在了，那么这次遍历一定会产生等差数列，因为当前的数字与之前的数字的差值也等于res，那么就会有起码3个元素等差。(如果发现公差相等，才可以找到若干个长度大于等于 3 的等差数列)
      hash[i].set(res, (hash[i].get(res) || 0) + l + 1); // 会出现重复数字等差的结果所以要加上自身
    }
  }
  return sum;
};
var numberOfArithmeticSlices = function (nums) {
  const hash = {};
  let sum = 0;
  for (let i = 0; i < nums.length; i++) {
    hash[i] = {};
  }
  for (let i = 1; i < nums.length; i++) {
    for (let j = 0; j < i; j++) {
      const res = nums[i] - nums[j];
      const l = hash[j][res] || 0;
      sum += l;
      hash[i][res] = (hash[i][res] || 0) + l + 1;
    }
  }
  return sum;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

这里我们可以发现用 map 来做的耗时远远小于用{}的方式， 从而科普一下 map 的优化

  1. 在 js 中，当你使用对象 object 时， 键 key 只能有 string 和 symbol 。然而 Map 的 key 支持的就比较多了，可以支持 string, symbol, number, function, object, 和 primitives

  2. size map 大小确定 map 只需要 o（1）,普通对象需要 o(n)，节省了大量空间

  3. 增删性能。map 不需要把所有的键转换为字符串，而 object 对象会。相比之下 map 节省了大量的性能

  4. 对象中的 key 是不保证顺序的，因为对于 number 是存放到 elements 中，会按照从小到大，对于字符串类型的是存放到 properties 中，会按照顺序添加。map 是保证顺序的，按照添加的顺序依次出来的。

  5. 原型链问题。普通对象继承了很多原型方法，如 toString。而 map 是干净的！

该题补充：

跟着示例 2 再走一遍：

输入：nums = new int[]{7, 7, 7, 7, 7}; 输出：16 状态数组如下：

[{}, {0=1}, {0=3}, {0=7}, {0=15}] 计算过程是这样的：

  • 下标 0，不累加；
  • 下标 1，不累加；
  • 下标 2，发现前面有一个 7（公差为 0），值是 1，加到结果中，res = 1；
  • 下标 3，发现前面有两个 7（公差为 0），值分别是 1 和 3，都加到结果中，res = 1 + 1 + 3 = 5；
  • 下标 4，发现前面有三个 7（公差为 0），值分别值 1、3、7，都加到结果中，res = 5 + 1 + 3 + 7 = 16。
编辑 (opens new window)
#算法#JavaScript
上次更新: 2023/03/22, 15:28:00
Leecode Easy算法
排序算法

← 排序算法→

最近更新
01
gsap动画库学习笔记 - 持续~
06-05
02
远程组件加载方案笔记
05-03
03
小程序使用笔记
03-29
更多文章>
Theme by Vdoing | Copyright © 2020-2023 CD | MIT License